FOC 学习 • WanHe's Notes

[TOC]

一.数学理论#

1.将三相随时间变换的相位差为120°的电流波形变换为三个间隔120°的矢量。

2.利用三角函数对矢量进行降维，降维到两个坐标轴。（就是投影）

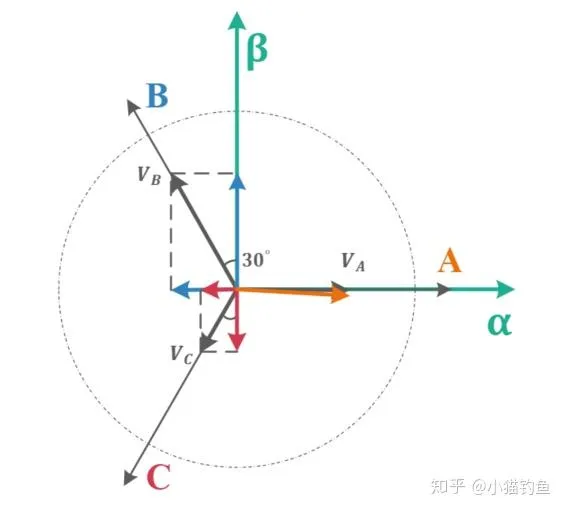
FOC Diagram

此为知乎大佬的图

这张图很清楚明显，根据我们的目的需要将abc三相电路投影到α与β所建立的直角坐标系上。

复杂的数学推理网上有很多讲得很好的资料和课程，我就偷懒直接上结果。

\left[ \begin{matrix} Iα\\ Iβ \end{matrix} \right]=\left[ \begin{matrix} 1&-\frac{1}{2}&-\frac{1}{2}\\ 0&\frac{\sqrt{3}}{2}&-\frac{\sqrt{3}}{2} \end{matrix} \right] \left[ \begin{matrix} i_a\\ i_b\\ i_c \end{matrix} \right]

当然这是变式中的一种

首先讲一下基尔霍夫电流定律（电路中任一个节点上，在任意时刻，流入节点的电流之和等于流出节点的电流之和）所以有：

简单说就是进去的水和出来的水是一样的

ia+ib+ic=0

根据这个定律可以通过一系列的数学变换发现，尽管矢量a与α轴重合，但是由于b,c相电流投影的存在，导致在a相输入1A电流，在α轴上的电流并不是等赋值的1A，而是- $\frac 32$ ，所以要乘上 $\frac 32$ 得到：

\left[ \begin{matrix} Iα\\ Iβ \end{matrix} \right]=\frac{2}{3}\left[ \begin{matrix} 1&-\frac{1}{2}&-\frac{1}{2}\\ 0&\frac{\sqrt{3}}{2}&-\frac{\sqrt{3}}{2} \end{matrix} \right] \left[ \begin{matrix} i_a\\ i_b\\ i_c \end{matrix} \right]

然后根据上面公式的关系以及基尔霍夫电流定律可以求得:

$I_α$ = $i_a$

然后进一步基于 $I_α$ = $i_a$ 与基尔霍夫电流定律可以求得 $I_β$ ：

I_β=\frac{1}{\sqrt{3}}\times(2i_b+i_a)

总结：

\begin{cases} I_β =i_α \\ I_β=\frac{1}{\sqrt{3}}\times(2i_b+i_a) \\ \end{cases}

其实关于clark逆变换的作用就是将降维后的形式重新升维变回原来的** $i_a,i_b,$$i_c$ 三相电流波形**。

将clark变换总结的公式可求得 $i_b$ :

i_b=\frac{\sqrt{3}I_β-I_α}{2}

根据基尔霍夫电流定律： $ia+ib+ic=0$ 得：

\begin{cases} i_a =I_α \\ i_b=\frac{\sqrt{3}I_β-I_α}{2} \\ i_c=\frac{-I_α-\sqrt{3}I_β}{2}\end{cases}

当然需要变换三次

首先了解一下前提，因为电机转子不断旋转，所以带动α与β回不断旋转，所以此时创建应该坐标系，将它固定到转子，当转子不断移动时坐标系也在不断移动。

一个定制来描述无刷电机的旋转

3.3-2

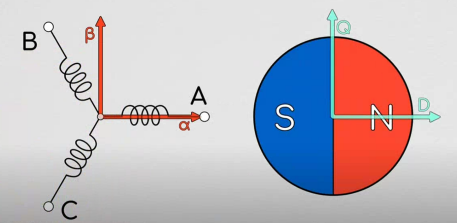
将此图结合就是下面的图

3.3-3

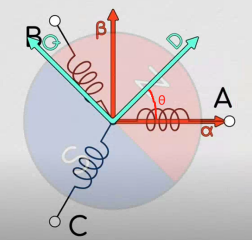
通过投影可以得到：

\left[ \begin{matrix} i_d\\ i_q \end{matrix} \right]=\left[ \begin{matrix} \cos\theta&\sin\theta\\ -\sin\theta&\cos\theta \end{matrix} \right] \left[ \begin{matrix} i_a\\ i_b\\ \end{matrix} \right]

通过矩阵乘法取逆得：

\left[ \begin{matrix} i_d\\ i_q \end{matrix} \right]=\left[ \begin{matrix} \cos\theta&\sin\theta\\ -\sin\theta&\cos\theta \end{matrix} \right]^{-1} \left[ \begin{matrix} i_a\\ i_b\\ \end{matrix} \right]

写为等式结果为：

\begin{cases} i_α=i_d\cos\theta-i_q\sin\theta\\ i_β=i_q\cos\theta-+i_d\sin\theta \end{cases}

通过 $I_q,I_d$ 和电角度求得 $I_α$ 和 $I_β$ 后，我们就可以通过前面提到的克拉克逆变换求得 $i_a,i_b,i_c$ 的波形,进而控制电机。

上面的数学理论主要讲解关于电流矢量，实际上电压矢量的推导过程是一致的。根据灯哥的视频里可以了解到这张图。

4.3-1